Typos are very common nowadays. When working in a fast-paced environment we expect computers to just understand what we mean intuitively, even if we didn't spell it out - sometimes literally in the form of spelling mistakes.
On this blog we've been through a deep dive into Levenshtein Automata, exploring how they are created using NFAs and Powerset Construction and finally diving deep into the Parameterized Levenshtein Automata to expose how professional search engines like Lucene handle fuzziness.
While Lucene can only fuzzy search with a maximum of 2 edits, today we review an algorithm which can handle up to 30 edits.
The algorithm was built while working on Levenshtypo, the library I developed and now maintain. It's used as the engine of Autypo, which I designed to be the idiomatic way to do autocomplete in .NET.
How it Works
In the lead-up to Parameterized Levenshtein Automata, I claimed that it is intractible for machines to execute NFA due to the potentially huge number of states. This claim is true if we assume that the machine were to consider each NFA state independently, as it would if the "active" NFA states were stored in a list.
Another way that a machine can represent an NFA is as bit strings, where each bit reflects whether the automaton is in a specific NFA state.
For example for an automaton with 8 possible NFA states, if we wanted to represent that the currently active states are either 3 or 5,
we would represent this as 0001 0100, which is a byte where the 3rd and 5th bit (right-to-left) are set.
In this world of bit strings, bitwise operations can be used to run NFA state transitions in parallel, slashing the running time of the algorithm down; critically no longer being related to active state count.
Encoding the NFA to Bits
Below is an example which regular readers will recall: a (non-paramerized) Levenshtein NFA representing 1 edit away from "et".
The red states represent the active states after processing 'e' as the first input character.
To represent the states as bits, each row is represented as a separate sequence of 3 bits.
The bits are show in most-significant order (right-to-left), such that the first bit 0 is at the
right of the bit string.
With this encoding, the bits representing the above NFA are:
010
011
The same encoding can be applied to Parameterized Levenshtein NFA. Consider the two below. If you were given a set of bits representing active states on the left, how would you transform them to the active states on the right?
The transformation can be done using a bitwise right shift operation. It will work regardless of which states are active. Remember to interpret bits right-to-left.
0010 >> 1 = 0001
0110 >> 1 = 0011
Recasting Automaton Operations as Bitwise Logic
We have just seen a bitwise right shift can be used to slide the window by a single character. In this section every action performed by Parameterized Levenshtein Automaton will be re-interpreted into bitwise operations.
The Transition function shown below computes the next NFA state based on the current NFA state and the Characteristic Vector.
To do so, it first follows each transition (match, insert, substitute, delete) as a separate operation.
Then, after some tidying-up, it checks if there are no active NFA state, in which case the input does not match.
Just like in Parameterized Levenshtein Automata, it calculates how far to slide the pattern window.
/// <summary>
/// Given the previous state, the characteristic vector and the automaton's edit distance,
/// calculates the next state.
/// </summary>
/// <param name="prevState">
/// Current automaton state. Index 0 represents e = 0, and so on.
/// </param>
/// <param name="characteristicVector">
/// Characteristic vector. Bit 0 (least significant) represents c 0, and so on.
/// </param>
/// <param name="edits">
/// Number of edits supported by the automaton.
/// </param>
/// <param name="nextState">
/// Next automaton state. Start at 0, will be populated by this method.
/// </param>
/// <returns>
/// isMatch: True if any state is still active.
/// slideFactor: The number of characters to advance the window.
/// </returns>
private static (bool match, int slideFactor) Transition(
uint[] prevState,
uint characteristicVector,
int edits,
uint[] nextState)
{
// Double-check a few invariants. Helps understand expectations.
Debug.Assert(prevState.Length == nextState.Length);
Debug.Assert(prevState.Length == edits + 1); // 0..e inclusive
// Follow "Matching" transitions
// TODO
// Follow "Insert" transitions
// TODO
// Follow "Substitute" transitions
// TODO
// Follow "Delete" transitions
// TODO
// Mask Bitmaps
// TODO
// Check that at least 1 state is active
bool anyActive = ...; // TODO
if (!anyActive)
{
return (false, slideFactor: default);
}
// Slide Window
int slideFactor = ...; // TODO
return (true, slideFactor);
}
Each // TODO is presented below as a small puzzle.
If you want, try to work it out before looking at the answer.
Its a great way to build intuition for how NFAs map onto bitwise logic.
Follow "Matching" transitions
The goal is to activate transitions from (c, e) to (c + 1, e) if the input character matches window[c].
Visual Example
The example diagram shows how the NFA on the left behaves when matching the Characteristic Vector 101.
The black transition represent the "match" operation, the others represent other operations and can be ignored.
Bitwise Encoding
Edits: 1
CharacteristicVector: 010
PrevState => NextState
[0]: 0001 => [0]: 0010
[1]: 0011 => [1]: 0010
Hint:
(c0, e0)matches on bit0, activating(c1, e0)(c0, e1)matches on bit0, activating(c1, e1)(c1, e1)has no matches
Answer
// Follow "Matching" transitions
for (var i = 0; i < nextState.Length; i++)
{
nextState[i] |= (prevState[i] & characteristicVector) << 1;
}
Follow "Insert" transitions
The goal is to activate transitions from (c, e) to (c, e + 1) in all cases.
Visual Example
The example diagram shows how the NFA on the left behaves for the insert transitions (marked in black). Remember to ignore other (grey) transitions for this operation.
Bitwise Encoding
Edits: 1
CharacteristicVector: not relevant
PrevState => NextState
[0]: 0011 => [0]: 0000
[1]: 0001 => [1]: 0011
Hint:
(c0, e0)activates(c0, e1)(c1, e0)activates(c1, e1)(c0, e1)has no insert transitions
Answer
// Follow "Insert" transitions
for (var i = 1; i < nextState.Length; i++)
{
nextState[i] |= prevState[i - 1];
}
Follow "Substitute" transitions
The goal is to activate transitions from (c, e) to (c + 1, e + 1) in all cases.
Visual Example
The example diagram has been expanded to an NFA of edit distance 2. It shows how the NFA on the left behaves for the substitute transitions (marked in black). Remember to ignore other (grey) transitions for this operation.
Bitwise Encoding
Edits: 2
CharacteristicVector: not relevant
PrevState => NextState
[0]: 000001 => [0]: 000000
[1]: 000110 => [1]: 000010
[2]: 000010 => [2]: 001100
Hint:
(c0, e0)activates(c1, e1)(c1, e1)activates(c2, e2)(c2, e1)activates(c3, e2)(c1, e2)has no substitute transitions
Answer
// Follow "Substitute" transitions
for (var i = 1; i < nextState.Length; i++)
{
nextState[i] |= prevState[i - 1] << 1;
}
Follow "Delete" transitions
This one is more complex than the previous, as each node has many delete transitions.
For d = 1 .. edits, each node (c, e) activates transitions to (c + 1 + d, e + d)
but only if the characteristic vector has bit c + d set.
We're looking to stick to a single for loop like the other operations, so try avoid nested loops if you can.
Visual Example
A visual example is much needed here. It shows how the NFA on the left behaves for the delete transitions (marked in black for 1 char deleted and orange for 2 chars deleted). Remember to ignore other (grey) transitions for this operation.
Notice how the (_, e0) states have 2 possible transitions. States with a higher e value would also
have multiple transitions if the target states existed.
Bitwise Encoding
Edits: 2
CharacteristicVector: 01100
PrevState => NextState
[0]: 000001 => [0]: 000000
[1]: 000101 => [1]: 000000
[2]: 000000 => [2]: 011000
Hint:
(c0, e0)activates(c3, e2)(c0, e1)has a delete transition but it does not match the characteristic vector(c2, e1)activates(c4, e2)
Answer
// Follow "Delete" transitions
uint deletionVector = prevState[0];
for (int i = 1; i < nextState.Length; i++)
{
nextState[i] |= (deletionVector << 2) & (characteristicVector << 1);
deletionVector = (deletionVector << 1) | prevState[i];
}
This one needs some explanation as it is trickier than the others.
Instead of using the previous states, we keep track of "deletion states".
In the diagram, focus on a single state for example (c3, e2).
It can be activated from either (c0, e0) and (c1, e1) with a vector matching 001000.
Hence, for the purposes of determining row e2, as long as either of those states is active then (c3, e2) will be activated.
The answer above avoids a nested loop by "carrying forward" active states onto the next row, "for free", using (c, e) => (c + 1, e + 1).
From there, we can simply deletion to (c, e) activating (c + 2, e + 1), if it matches character c + 1.
In other words, (c0, e0) first silently activates (c1, e1), which in turn activates the deletion transition to (c3, e2).
Mask Bitmap
Edit distance 1 requires a bitstring of length 4, 2 of length 6 and so on.
As bits are grouped into 8 (byte, ushort, uint, ulong) there is a chance
that an "invalid" bit might be set.
It's best to just clear any bits which are not part of the bitstring, as we would not want to accidentally move it back into the window when sliding it.
Bitwise Encoding
Edits: 2
CharacteristicVector: not relevant
NextState (before) => NextState (after)
[0]: 00 000001 => [0]: 00 000001
[1]: 00 000101 => [1]: 00 000101
[2]: 01 010000 => [2]: 00 010000
Answer
// Mask Bitmaps
var windowLength = 2 * edits + 2; // 0 .. 2n+1 (inclusive)
uint mask = (1u << windowLength) - 1; // All bits in windowLength set to 1
for (int i = 0; i < nextState.Length; i++)
{
nextState[i] &= mask;
}
Check >= 1 State is Active
A straightforward implementation of this would be to check whether any states are non-zero.
Can you think of a bitwise operation to combine the states in a for loop, making a if check after the
loop?
Bitwise Encoding
Edits: 2
CharacteristicVector: not relevant
NextState Example 1, AnyActive = true
[0]: 000001
[1]: 000101
[2]: 010000
NextState Example 2, AnyActive = false
[0]: 000000
[1]: 000000
[2]: 000000
Answer
// Check that at least 1 state is active
uint combined = 0u;
for (int i = 0; i < nextState.Length; i++)
{
combined |= nextState[i];
}
bool anyActive = combined is not 0u;
if (!anyActive)
{
return (false, slideFactor: default);
}
Slide Window
This operation must first determine the number of characters to advance the window. The state must then be updated to reflect the sliding window, a bitwise operation which we have already seen.
Bitwise Encoding
Edits: 2
CharacteristicVector: not relevant
NextState (before) => NextState (after)
[0]: 000010 => [0]: 000001
[1]: 001010 => [1]: 000101
[2]: 100000 => [2]: 010000
Answer
// Slide Window
uint combined = 0u; // same loop as the last puzzle
for (int i = 0; i < nextState.Length; i++)
{
combined |= nextState[i];
}
// TrailingZeroCount counts the number of `0`s at the end of the combined state flag.
int slideFactor = (int)uint.TrailingZeroCount(combined);
if (slideFactor > 0)
{
for (int i = 0; i < nextState.Length; i++)
{
nextState[i] >>= slideFactor;
}
}
Putting it Back Together
It would be sufficient to just copy the various answers back into the Transition function.
In addition to that, the listing below merges the for loops together for matching, inserting, substituting, deleting, masking, and buliding the combined state.
int windowLength = 2 * edits + 2; // 0 .. 2n+1 (inclusive)
uint mask = (1u << windowLength) - 1; // All bits in windowLength set to 1
uint deletionVector = 0u;
uint combined = 0u;
for (var i = 0; i < nextState.Length; i++)
{
uint next = (prevState[i] & characteristicVector) << 1; // Match transition
if (i > 0) // Hoist i == 0 out of the loop to avoid this "if test"
{
next |= prevState[i - 1]; // Insert transition
next |= prevState[i - 1] << 1; // Substitute transition
next |= (deletionVector << 2) & (characteristicVector << 1); // Delete transition
}
deletionVector = (deletionVector << 1) | prevState[i];
next &= mask;
nextState[i] = next;
combined |= next;
}
if (combined is 0u)
{
return (false, slideFactor: default);
}
// TrailingZeroCount counts the number of `0`s at the end of the combined state flag.
int slideFactor = (int)uint.TrailingZeroCount(combined);
if (slideFactor > 0)
{
for (int i = 0; i < nextState.Length; i++)
{
nextState[i] >>= slideFactor;
}
}
return (true, slideFactor);
Creating the DFA
The transition function we created above contains most of the logic we need. It does, however, need to be encapsulated correctly to be usable as a DFA.
In this section we encapsulate the logic into a BitwiseLevenshteinAutomaton class.
It's given the editDistance and the pattern upon creation, and in turn initializes the current state as a uint[] with (c0, e0) set,
as well as aligning the window to the first pattern character.
public class BitwiseLevenshteinAutomaton(int editDistance, string pattern)
{
private uint[] _currentState = InitialState(editDistance);
private int _windowStartIndex = 0;
private static uint[] InitialState(int editDistance)
{
var result = new uint[editDistance + 1];
result[0] = 1u;
return result;
}
public bool Transition(char inputChar) => ...; // TODO
public bool IsAccepting => ...; // TODO
}
As always for DFAs in this series so far, we add the Reset and Clone methods.
/// <summary>
/// Returns a new automaton ready to match a new string with the same pattern.
/// </summary>
public BitwiseLevenshteinAutomaton Reset() => new BitwiseLevenshteinAutomaton(editDistance, pattern);
/// <summary>
/// Returns a new automaton in the same state as this one.
/// </summary>
public BitwiseLevenshteinAutomaton Clone()
{
var clone = new BitwiseLevenshteinAutomaton(editDistance, pattern);
clone._currentState = (uint[])_currentState.Clone();
clone._windowStartIndex = _windowStartIndex;
return clone;
}
Transition
The public overload of Transition accepts an input character to modify the internal state then return whether the
input string can still match.
It is implemented by building up the parameters to the private Transition method.
The pattern is first narrowed to the window using the offset and length.
inputChar is then compared to each of the window characters, creating the Characteristic Vector.
From there the rest of the method should be relatively easy to follow.
public bool Transition(char inputChar)
{
// First we build the characteristic vector
var remainingPatternChars = pattern.Length - _windowStartIndex;
var windowLength = Math.Min(2 * editDistance + 1, remainingPatternChars);
var window = pattern.AsSpan(_windowStartIndex, windowLength);
var characteristicVector = CreateCharacteristicVector(inputChar, window);
// Initialize the next state
var nextState = new uint[editDistance + 1];
// Run the transitions
var (isMatch, slideFactor) = Transition(_currentState, characteristicVector, editDistance, nextState);
// Update the internal state
_currentState = nextState;
_windowStartIndex += slideFactor;
return isMatch;
}
// Examples (bits are RightToLeft)
// ('e', "egg") => 0b001
// ('g', "egg") => 0b110
private static uint CreateCharacteristicVector(char inputChar, ReadOnlySpan<char> window)
{
uint result = 0;
for (var i = 0; i < window.Length; i++)
{
if (inputChar == window[i])
{
result |= 1u << i;
}
}
return result;
}
IsAccepting
A state is accepting if it reaches the final column - or if it can consume remaining edits to reach it.
As an example, consider the diagram below which shows the state after the input "her" is matched against the pattern "here"
(the final 'e' is missing).
We would also reach this state after processing the first three characters of the input "hers".
However, in this case the automaton would then process the 's' and follow the (black) diagonal transition to the final state (c1, e1).
Both of these cases are equally 1 edit distance - "her" is missing a letter and "hers" has a substituted letter.
To simulate the missing input characters, the automaton can activate the substitution transitions anyway. This allows the automaton to reach a final state even when missing the final characters.
Hence: Before testing the final states, we recursively activate
(c, e)=>(c + 1, e + 1)to account for trailing deletions.
/// <summary>
/// If true then the automaton is in a state representing successful match.
/// </summary>
public bool IsAccepting
{
get
{
var remainingPatternChars = pattern.Length - _windowStartIndex;
if (remainingPatternChars > 2 * editDistance + 1)
{
// Too far from the end to possibly accept
return false;
}
uint finalVector = 0;
for (var i = 0; i < _currentState.Length; i++)
{
// Recursively activate the diagonal transitions
finalVector = (finalVector << 1) | _currentState[i];
}
// Acceptance requires reaching at least the last column
uint threshold = 1u << remainingPatternChars;
return finalVector >= threshold;
}
}
Implementation Notes
The above code is a complete implementation of the bit-parallel execution of the Levenshtein NFA. There are, however, a few implementation details which make it sub-optimal for real use-cases.
The bit strings were all encoded within 32-bit uints. Edit distance of 1 to 3 can fit in a byte,
4 to 7 in a ushort, 8 to 15 in a uint, and 16 to 30 in a ulong.
Practical implementations should carefully choose the right data type for the use-case.
The NFA state was represented as arrays (uint[]) which in .NET are costly heap allocations subject
to garbage collection. A practical implementation should attempt to reduce these and allocate them on
the stack instead.
In Levenshtypo, a .NET implementation,
both of these concerns were solved.
Generic Math was used to parameterize the data type (byte vs ushort vs ...) and
Inline Buffers to allocate the NFA state on the stack as a struct.
Hence Levenshtypo will be used in the coming benchmarks, as opposed to the blog-quality code shown above.
Evaluating The Claim
15 times fuzzier than Lucene is a bold claim - but is it fair?
While it's an objective fact that 30 edits is 15 times more Lucene's 2 edits, the spirit of the claim implies comparable efficiency.
In this section we will focus on whether the bit-parallel algorithm described above is efficient enough to be used in near-instant fuzzy search.
Let's evaluate the algorithm from a few practical angles: memory usage, throughput, and real-world applicability
N.B. Annoyingly, a review of the scientific literature reveals that I may not be the first to "discover" this algorithm, so I refrain from making that claim.
Real-World Applicability
I also want to clarify that I'm not trying to bash Lucene. It's an incredibly well-made and ambitious tool and is extremely well known - making it a great benchmark. The vast majority of use-cases are well covered by a fuzziness of 2 edits, especially when using Restricted Edit Distance. The way Lucene hardcodes the Parameterized Levenshtein DFAs directly into their code-base is an insanely efficient approach. It is, however, undeniable that there will be some use-cases for which more than 2 edits is a hard requirement. This algorithm is for those cases.
Memory Usage
The canonical use-case for Levenshtein Automata in Fuzzy Search is searching a Trie using Depth-First Search.
Briefly, Depth-First Search maximises efficient stack allocations by recursively exploring child nodes of the Trie. Recursion occurs at least whenever a node has multiple children; in this case the node is kept on the stack and child nodes are explored using further stack frames.
Professional implementations will be aware of the risk of too much recursion - overflowing the stack memory - and will have measures to break recursion by allocating on the heap. This approach provides a balance between the efficient stack and the plentiful heap.
For the purposes here, we can err on the side of pessimism, assuming each character requires a stack frame on which the entire NFA state is stored. Searching a word of 10 characters will require 10 copies of the NFA state.
The graphs below show how many bytes are required to represent the current automaton state as edit distance increases.
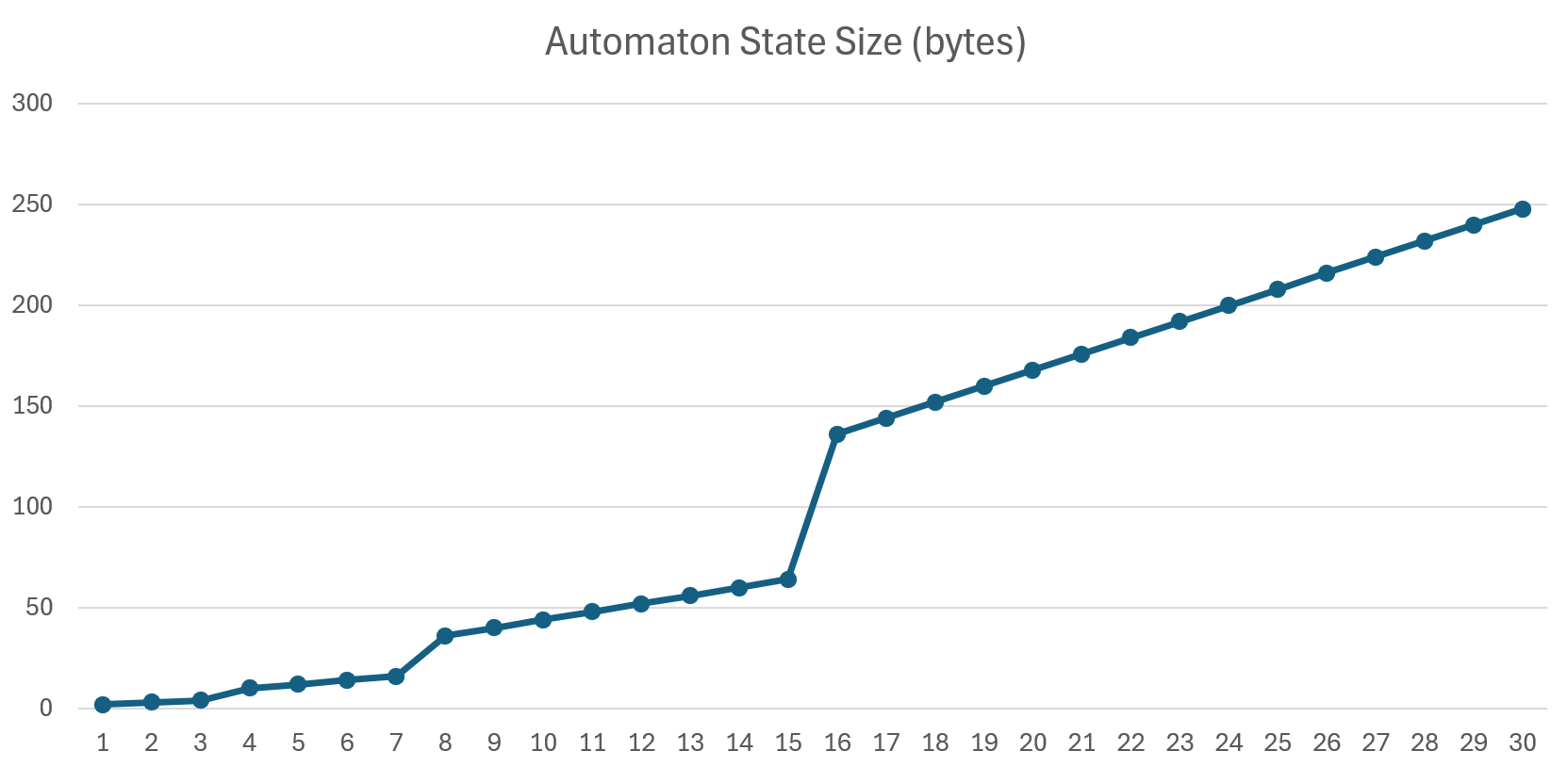
For example, 16 bytes are required to represent the state of the automaton for edit distance of 7. At the upper end, searching with edit distance 30 requires a massive 248 bytes to hold the current state.
An analysis of the memory usage reveals why Powerset Construction is such a useful algorithm for executing NFA...
Powerset Construction creates a DFA state only for reachable combinations of NFA states.
For a Parameterized Levenshtein Automaton matching 4 edits there are 50 NFA states (c0 e0 to c10 e4).
If every possible combination was reachable there would be around 2 ^ 50 combinations.
Powerset Construction identifies that only 1353 (~ 2 ^ 11) combinations are reachable.
Already for edit distance 4, if the DFA were not pruned to remove unreachable states, then there would be more DFA states than
uint.MaxValue.
Repeating the analysis for edit distance 30 shows there are 1922 NFA states (c0 e0 to c61 e30) leading to 2 ^ 1922 combinations.
If we were to assign each NFA state to a single bit ("active" or "inactive"), it would take 241 bytes to represent all states.
The bit-parallel algorithm can achieve such high fuzziness in part because it does not prune unreachable states (which would be intractable). As a result it must be able to represent unreachable states, accounting for the significant memory usage.
Throughput
The usual benchmarks in this series have measured how long it takes to search for a word in a dataset of 450,000 English words. This will not really be helpful with an edit distance of 30 because nearly every single word would match. In the benchmark below I've modified each word including the search word to repeat each character many times (proportional to edit distance). This should keep a comparable result set size.
The table below shows the performance of different automata implementations:
- Bit Parallel is the algorithm described in this article, edit distances from 1 to 30.
- Parameterized (Hardcoded) uses the hardcoded states of Parameterized Levenshtein Automata, the same as Lucene does, edit distances 1 and 2.
- Parameterized runs Powerset Construction to build the Parameterized Levenshtein Automata at runtime.
The implementations are available for review on the Levenshtypo library GitHub page.
| Method | Edit Distance | Mean | Heap Allocated |
|---|---|---|---|
| Parameterized (Hardcoded) | 1 | 23.27 us | 400 B |
| Parameterized (Hardcoded) | 2 | 28.63 us | 400 B |
| Parameterized | 1 | 26.90 us | 496 B |
| Parameterized | 2 | 31.58 us | 496 B |
| Parameterized | 3 | 42.50 us | 496 B |
| Parameterized | 4 | 43.95 us | 496 B |
| Bit Parallel | 1 | 35.29 us | 400 B |
| Bit Parallel | 2 | 52.59 us | 400 B |
| Bit Parallel | 3 | 65.20 us | 400 B |
| Bit Parallel | 4 | 96.13 us | 432 B |
| Bit Parallel | 5 | 119.65 us | 432 B |
| Bit Parallel | 6 | 145.52 us | 464 B |
| Bit Parallel | 7 | 166.72 us | 464 B |
| Bit Parallel | 8 | 176.55 us | 528 B |
| Bit Parallel | 9 | 207.64 us | 560 B |
| Bit Parallel | 10 | 233.77 us | 560 B |
| Bit Parallel | 15 | 454.14 us | 656 B |
| Bit Parallel | 20 | 757.98 us | 1072 B |
| Bit Parallel | 25 | 1,103.97 us | 1233 B |
| Bit Parallel | 30 | 1,478.37 us | 1393 B |
For Edit Distances 1-4 there are directly comparable data points for Bit Parallel vs Parameterized. These indicate that the Bit Parallel approach is between 30% and 100% slower than the Parameterized approach. As the Parameterized approach is blazingly fast it can be argued that the Bit Parallel approach is probably also suitable for fuzzy search.
As the maximum edit distance increases, it becomes increasingly slower. At the extreme end, a 30-edits search with Bit Parallel is 42 times slower than a 1-edit search. A lot of this comes not only from more inner loops, but a larger characteristic vector which must be compared against more window characetrs, worse memory locality, and increased zeroing of data.
However, I'd argue that considering the extreme degree of fuzziness, 1.5 milliseconds to search 450,000 entries is pretty good.
This argument relies on the assumption that using such a large edit distance will not match most of the entries - in which case a lot of the benefits are lost.
Conclusion
In this article we discussed how to use bitwise operations to execute the NFA of the Parameterized Levenshtein Automata directly, avoiding powerset construction (the costly part).
By avoiding powerset construciton we end up having to model all possible states, even if they are unreachable. This creates some costly memory requirements, and a state which is more expensive to operate on than a simple integer as in the Parameterized approach.
The Bit Parallel algorithm described in this article delivers on the premise that degrees of fuzziness significantly larger than 2 are achievable in practice. Perhaps 30 is a stretch, but I would argue that the cut-off is somewhere in between.







Join the Discussion
You must be signed in to comment.