Have you wondered how your phone knows how to correct your typos as you type? Fuzzy Search! Have you searched "resrtaurants near me" and Google knows exactly what you mean? Also Fuzzy Search! Fuzzy Search is when a program looks for words which almost match some input.
But how does that actually work? In this article we will explore the data structures which are at the core of many of the fuzzy search engines we use today, Tries and Levenshtein Automata. Throughout the post we will implement these data structures in C#, and by the end be able to run a functional and algorithmically efficient fuzzy search which in 30 microseconds can find all English words similar to an input string.
Similarity Metrics
Fuzzy search requires looking for strings which are similar to some input. To know what to look for, an algorithm needs to measure "similarity". A Similarity Metric is a function which compares two strings and quantifies their similarity. Different similarity metrics prioritize different aspects; one metric might treat similar sounds as minor errors whilst other metrics might use the distance between typical keyboard layout as a baseline. After all, "tine" is much more likely to be a misspelling of "time" than of "vine".
One of the most prolific Similarity Metrics is Levenshtein Distance,
which counts the number of edits (insertions, deletions, substitutions) needed to transform from one string into another.
For example to transform "et" into "eat" requires 1 edit (inserting the character 'a').
"eaat" is also only 1 Levenshtein Distance from "eat" as it requires a single deletion of the duplicate 'a'.
Implementing Levenshtein Distance efficiently is actually a common way to introduce the concept of Dynamic Programming.
However, since it is not necessary to understand the algorithm for fuzzy search, and as there are many other online
articles which cover that exact topic very well, I won't be doing so here.
Levenshtein Distance is so widely used in part because it is easy to compute, and also because it is domain-agnostic (it's probably good enough in many places). This unfortunately does mean that for many problems Levenshtein Distance is simply not the best measure for string similarity. Jaro Winkler distance considers strings which match earlier on as more similar due to how humans perceive words. Restricted Edit Distance adds swapping adjacent letters as an edit on top of Levenshtein Distance.
Nevertheless, the rest of the article uses Levenshtein Distance as the similarity metric (many of the concepts can be re-used for other metrics). Therefore we can more formally define the problem of Fuzzy Search used below:
Given a query and many pre-indexed strings, find the ones which have the lowest Levenshtein Distance from the query.
Finite State Automata
A Finite State Automaton (FSA) is a simple yet powerful tool for matching strings, used in everything from regular expressions to compilers to fuzzy search. FSAs are best represented graphically with the following rules (which I have simplified for the purposes of this article):
- The FSA starts in the starting state
- Read a character from the input string and follow the matching arrow to find the next state
- If there is no matching arrow, the input string is not recognised by the FSA.
- Repeat this step until there are no more characters in the input string
- If the final state after all characters is an "accepting" state, then the input string is recognised by the FSA.
In this article we will used the convention that the starting state is the green circle and accepting states have a blue outline. Review the 3 examples of FSAs in the image below. They represent the same thing as the regular expressions:
"a"-> only match the string"a""a+"-> match one or more'a'characters"a(bc)*"-> match an'a'followed by zero or more pairs of"bc"s, but never a"b"or a"c"in isolation
It's no accident to use Regular Expressions to compare the language accepted by a FSA. In Computer Science, it's well established that FSAs and Regular Expressions have the exact same expressivity - i.e. for every FSA there is a Regular Expression and vice versa.
To implement an FSA in C#, we will first define what a FsaState class.
/// <summary>
/// Represents a state which can be reached by an Automaton.
/// </summary>
public class FsaState
{
/// <summary>
/// Defines a mapping for the next state which should be
/// assumed when encountering specific characters.
/// </summary>
public Dictionary<char, int> Transitions { get; } = new();
/// <summary>
/// We're skipping ahead here but it will come in handy later.
/// When non-null, defines the state which should be assumed
/// if no characters match <see cref="Transitions"/>.
/// </summary>
public int? WildcardTransition { get; set; }
/// <summary>
/// If the FSA is in this state after all characters have been
/// read, then this defines whether the input string was
/// accepted or not.
/// </summary>
public bool IsAccepting { get; set; }
}
A FiniteStateAutomaton class stores a list of possible states, and can be in a single
state at any one time.
/// <summary>
/// Represents an automaton which exists in a single state
/// </summary>
public class FiniteStateAutomaton(FsaState[] states)
{
// An automaton must always be in exactly 1 state.
// We use the convention that the first state (index 0) is the initial state.
private int _currentStateIndex = 0;
/// <summary>
/// If true then the automaton is in a state representing successful match.
/// </summary>
public bool IsAccepting => states[_currentStateIndex].IsAccepting;
}
At this point the automaton isn't very useful as it needs a way to transition to different states. This can be done by inspecting the current state's transition dictionary or falling back to the wildcard. Here's one possible implementation:
/// <summary>
/// Advances the automaton based on the input symbol.
/// </summary>
public bool Transition(char input)
{
var state = states[_currentStateIndex];
if (state.Transitions.TryGetValue(input, out var nextStateIndex))
{
// This is the simple case - there is a transitions specifically for this character
_currentStateIndex = nextStateIndex;
return true;
}
if (state.WildcardTransition is { } wildcard)
{
// The state has a specific transition for all characters
// which aren't mapped explicitly above.
_currentStateIndex = wildcard;
return true;
}
// There is no transition defined for this character, so
// we will never get to an accepting state.
return false;
}
With that we already have a fully functional automaton. To create the automata we have seen earlier we can use the following code
// Regex: "a"
var automaton1 = new FiniteStateAutomaton([
new FsaState { Transitions = { { 'a', 1 } }, IsAccepting = false },
new FsaState { Transitions = { }, IsAccepting = true }
]);
// Regex: "a+"
var automaton2 = new FiniteStateAutomaton([
new FsaState { Transitions = { { 'a', 1 } }, IsAccepting = false },
new FsaState { Transitions = { { 'a', 1 } }, IsAccepting = true }
]);
// Regex: "a(bc)+"
var automaton3 = new FiniteStateAutomaton([
new FsaState { Transitions = { { 'a', 1 } }, IsAccepting = false },
new FsaState { Transitions = { { 'b', 2 } }, IsAccepting = true },
new FsaState { Transitions = { { 'c', 1 } }, IsAccepting = false }
]);
Levenshtein Automata
Now that we understand how Finite State Automata work, we can explore how they are applicable to Fuzzy Search. A Levenshtein Automata is a FSA where the states are configured to answer the following question (for some pre-defined string S and an edit distance E):
Is the Levenshtein distance between the input string and S less than or equal to E? Yes / No
Show below is a visual representation of a simple Levenshtein Automaton, accepting strings
which are within 1 edit distance of the string "et".
The same rules as discussed earlier apply, but the automata may also follow arrows matching
'*' if and only if no other arrow matches.
To internalise the concept, try out some matching strings like
"et","eat","let", and some non-matching ones like"best","eats","sty".
Try it programmatically:
var is1LevenshteinDistanceFromEt = new FiniteStateAutomaton([
new FsaState { Transitions = { { 'e', 1 }, { 't', 5 } }, WildcardTransition = 7, IsAccepting = false }, // 0 start
new FsaState { Transitions = { { 't', 2 } }, WildcardTransition = 3, IsAccepting = true }, // 1 e
new FsaState { Transitions = { }, WildcardTransition = 4, IsAccepting = true }, // 2 et
new FsaState { Transitions = { { 't', 4 } }, WildcardTransition = null, IsAccepting = true }, // 3 e*
new FsaState { Transitions = { }, WildcardTransition = null, IsAccepting = true }, // 4 et* e*t tt tet *et *tt
new FsaState { Transitions = { { 't', 4 }, { 'e', 6 } }, WildcardTransition = null, IsAccepting = true }, // 5 t
new FsaState { Transitions = { { 't', 4 } }, WildcardTransition = null, IsAccepting = false }, // 6 te
new FsaState { Transitions = { { 'e', 6 }, { 't', 4 } }, WildcardTransition = null, IsAccepting = false }, // 7 *
]);
Console.Write("Enter a string to see if it is within 1 Levenshtein Distance from \"et\": ");
var input = Console.ReadLine() ?? string.Empty;
var match = Accept(is1LevenshteinDistanceFromEt, input);
Console.WriteLine($"Lev(\"et\", \"{input}\"): {(match ? "TRUE" : "FALSE")}");
static bool Accept(FiniteStateAutomaton automaton, string input)
{
foreach (char charInput in input)
{
if (!automaton.Transition(charInput))
{
return false;
}
}
return automaton.IsAccepting;
}
You may have noticed that some of the states can be reached via multiple paths, for example "eat" and "let" both end in the same state. This happens because the underlying state represents the same scenario no matter how it got there; in both cases the current string is acceptable but only if no more characters are read.
Building the FSA to match a specific Levenshtein Automaton involves many of these logical deductions. Including it here, however, would not improve the understanding of how they are used in Fuzzy Search, and as it is a complex topic that deserves it's own deep dive, I plan to cover in a future blog post.
As a peek into the complexities of Levenshtein Automata construction, though, a visual example may help. Below is one matching 2 edit distance from the word "parallelogram". The take away here is that these graphs can grow in complexity very quickly, so optimization is key.
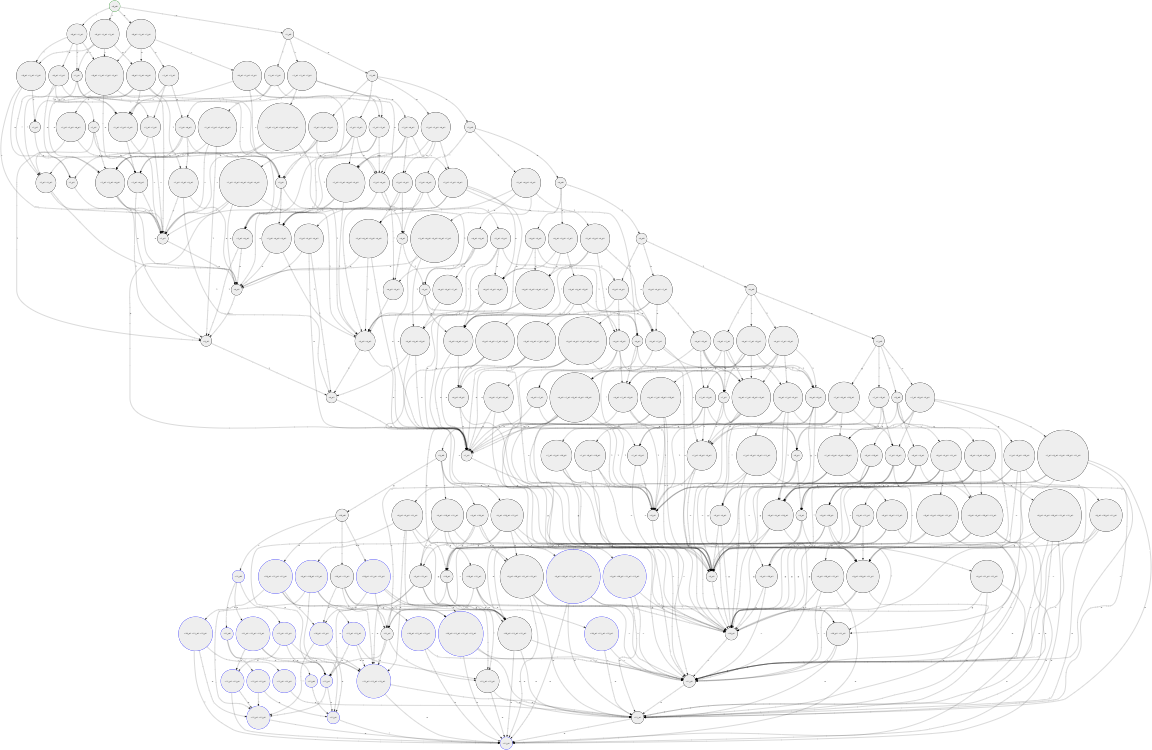
Even at this initial level of understanding, Levenshtein Automata can offer significant performance advantages over directly computing the Levenshtein Distance, especially if one input string must be tested against many others to find similar strings. To highlight just how efficient they are, I benchmarked the code in this blog post against Quickenshtein, one of the fastest .NET Levenshtein distance calculators.
Scenario: Find all English words which are within 1 edit distance from
"et".
| Method | Mean | Error | StdDev |
|---|---|---|---|
| FindWords_Automata_Blog | 6.008 ms | 0.1195 ms | 0.1377 ms |
| FindWords_Quickenshtein | 43.647 ms | 0.3602 ms | 0.3369 ms |
Whilst it's important to highlight that the benchmark is designed to highlight the strengths of the Automata solution, the results were still striking. The blog-quality Levenshtein Automaton performed 7 better times than the optimized .NET library did when over 450,000 words were searched sequentially. This works because the Levenshtein Automata stop processing strings once it is clear they can't match (no need to look past the second typo). The absolute numbers aren't important, but the take away should be that Levenshtein Automata are very fast for their intended use-cases.
To use Levenshtein Automata in a production environment, I'd recommend Levenshtypo, the library I created for just this purpose. The main project page shows some great benchmarks - check them out.
The benchmark does reveal that more work is needed before we understand fuzzy search. While 6 milliseconds is impressive for 450,000 words, it's not fast enough. To understand how we can bring that down to roughly 30 microseconds (200 times faster), we need to use Tries.
Tries
A Trie is a graph data structure with a single root node and edges labelled by characters. To find a word in a Trie, the program follows the edges matching the characters until all characters have been processed. The final node may have associated data such as some index into the document text.
Tries are also widely used in routing (e.g., ASP.NET) and other performance-critical systems.
Here's how a Trie stores the strings ["a", "at", "ate", "ear", "eat", "eats"].
To find the word "ear" we follow the edges 'e', then 'a', then 'r', to land on the "ear" node where
metadata about that word will be stored.
Let's implement a very straightforward Trie. We define a TrieNode class which links to it's child nodes
and optionally has a value.
public class TrieNode
{
public Dictionary<char, TrieNode> Children { get; } = new();
public object? Value { get; set; }
}
The Trie class wraps many nodes by holding on to the root. It also has logic to find a node based on some input.
This FindNode method can be implemented recursively by taking the first character off the string, finding the
right child node, and passing the remainder of the string to the next method call. An empty string indicates that
the program has found the node.
public class Trie
{
private readonly TrieNode _root = new();
private TrieNode? FindNode(ReadOnlySpan<char> input, TrieNode node, bool create)
{
if (input.IsEmpty)
{
// We have consumed the whole string so return the node.
return node;
}
var head = input[0];
if (!node.Children.TryGetValue(head, out var nextNode))
{
if (create)
{
// Add a new edge to a new node
node.Children.Add(head, nextNode = new TrieNode());
}
else
{
return null;
}
}
return FindNode(input[1..], nextNode, create);
}
}
Finally, we will need a very simple public API to get and set values. Hopefully the code is self-explanatory.
public object? Get(string input)
{
TrieNode? trieNode = FindNode(input, _root, create: false);
return trieNode?.Value;
}
public void Set(string input, object value)
{
var node = FindNode(input.AsSpan(), _root, create: true)!;
node.Value = value;
}
We can create the trie shown in the diagram earlier as follows:
var trie = new Trie();
trie.Set("a", "a");
trie.Set("at", "at");
trie.Set("ate", "ate");
trie.Set("ear", "ear");
trie.Set("eat", "eat");
trie.Set("eats", "eats");
It's also worth noting that there are many variants of the Trie data structure which focus on improving different aspects such as space utilization, update speed and read speed. The above simplistic approach is the easiest to understand and visualize but is rarely used in production systems.
Combining Both Structures
At this point we must consider the similarities between Tries and Levenshtein Automata. They both:
- Are graphs with edges labelled by single characters
- Start at an initial node
- Consume characters in the input string by following edges in the graph
- Contain insights about the input string at the final node after all characters have been consumed
Walking both graphs involves running both graphs simultaneously - only exploring Trie nodes which could lead to
an accepting state in the Levenshtein Automaton.
Let's consider a scenario where the user has entered the string "et". To find matching words, we would
construct the Levenstein Automaton shown earlier and find all matching Trie nodes.
Below is what this would look like if using the above Trie example.
root (state: root)
├─ a (state: *)
│ └─ at (state: *t) ──► match - FOUND
│ └─ ate (state: not found) ──► skip
└─ e (state: e) ──► match but not a word
└─ ea (state: e*) ──► match but not a word
├─ ear (state: not found) ──► skip
└─ eat (state: e*t) ──► match - FOUND
To achieve this programmatically we must first add Clone to FiniteStateAutomaton.
This will be a convenient way to avoid mutating different paths through the tree.
public class FiniteStateAutomaton
{
// The rest of the class is the same as earlier, but
// to it we add a new method "Clone".
/// <summary>
/// Returns a new automaton in the same state as this one.
/// </summary>
public FiniteStateAutomaton Clone()
{
var clone = new FiniteStateAutomaton(states);
clone._currentStateIndex = _currentStateIndex;
return clone;
}
}
For the final code block in this article, we will implement FuzzySearch on the Trie class.
FuzzySearch is similar to FindNode, but consults the Levenshtein Automaton to know whether
to visit a child nodes.
public class Trie
{
public IEnumerable<object> FuzzySearch(FiniteStateAutomaton automaton)
{
var results = new List<object>();
FuzzySearch(automaton, _root, results);
return results;
}
private void FuzzySearch(FiniteStateAutomaton automaton, TrieNode node, List<object> results)
{
if (automaton.IsAccepting && node.Value is { } value)
{
results.Add(value);
// We don't exit here - a child node might still
// match the automaton, possibly even better than
// this node does.
}
foreach (var (c, childNode) in node.Children)
{
// We clone the automaton to avoid one branch affecting another.
var clonedAutomaton = automaton.Clone();
if (clonedAutomaton.Transition(c))
{
FuzzySearch(clonedAutomaton, childNode, results);
}
}
}
}
This approach correctly identifies "at" and "eat" as the two words within 1 edit distance of "et".
This is exactly how search engines do fuzzy search. Before you've typed in the first query, the search engine has already built it's internal index into a Trie (variant). Most engines persist the index on external storage so that it is ready to go immediately when the program starts.
Then the queries start coming into the system. Whenever a word needs to be matched inexactly, the engine
builds an automaton to represent that. Some search engines vary the fuzziness based on the length of the
string; for example "hello" would typically allow a single typo whereas "parallelogram" might allow for
more. In any case the query is represented by an automaton which is run against the Trie.
The Trie nodes which are also in accepting states are considered matching and the metadata stored is used in conjunction with other contextual information to satisfy the query. Depending on how the engine is designed, the metadata could be a token identifier or some inverted index into which documents contain that token, or really anything else.
Conclusion
Hopefully next time you're tapping in keys at lightning-fast speed and your phone is cleaning up the letter salad you've left behind, you'll have a better understanding how it does that so quickly.
After understanding how Levenshtein Automata can outperform some of the fastest Levenshtein Distance libraries in the .NET ecosystem, even when using blog-quality coding, you'll start to wonder how they're constructed so quickly. It's a very complex topic though - not even Lucene's original developers wanted to venture there.
When you feel satisfied that Tries are deceptively simple yet powerful, it may surprise you to learn how many variants have been documented, each specialized for different strengths.
.NET implementations of all of the above concepts are available publicly via the Levenshtypo library which powers Autypo, an autocomplete library created as an idiomatic way to do autocomplete in .NET.



Join the Discussion
You must be signed in to comment.